
The combat against HIV, the virus responsible for AIDS has witnessed consistent advancements and studies put forward by researchers in various fields. To identify a more intelligent and effective approach to combat HIV-1 and enhance the understanding of the workings of its treatments, Dr Koyel Chakravarty, Assistant Professor, Department of Mathematics has published a paper titled “Mathematical modelling of HIV-1 transcription inhibition: a comparative study between optimal control and impulsive approach” in the Q2 journal, Journal of Computational and Applied Mathematics.
Abstract
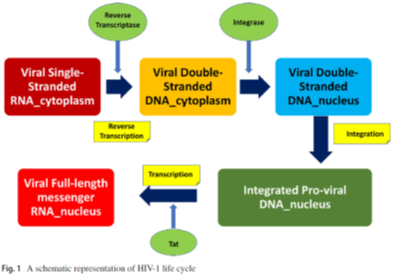
By adopting a proactive strategy, this study facilitates the interaction with human immunodeficiency virus type I (HIV-1), successfully navigating its sequential fusion stages. This approach enables efficient infiltration of the virus into a target CD4+T helper cell within the host organism, initiating the virus’s replication cycle. As a retrovirus, HIV-1 orchestrates the conversion of its single-stranded viral RNA genome into a more stable double-stranded DNA structure. The newly formed DNA integrates with the host cell’s genetic material, and the pro-viral DNA transforms into functional messenger RNA (mRNA) with the assistance of the host enzyme RNA polymerase II (Pol II).
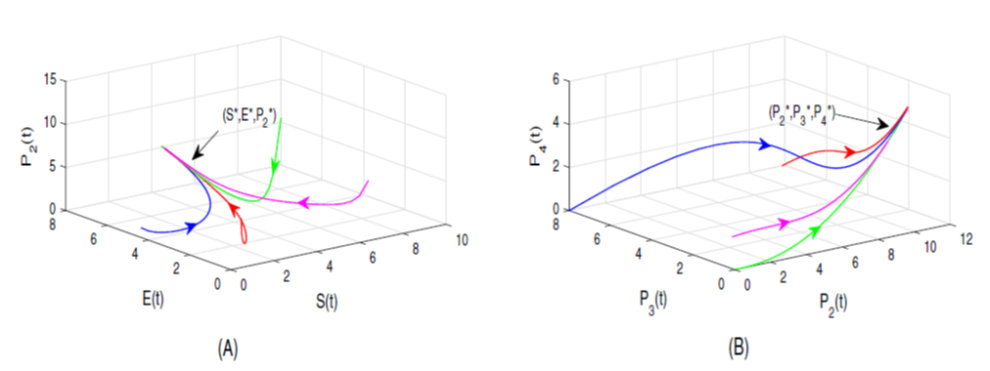
The ongoing research focuses on constructing a meticulous mathematical framework using a system of nonlinear differential equations. The investigation aims to assess the impact of a Tat inhibitor on suppressing the transcriptional activity of HIV-1, treating it as an optimal control problem. The study also evaluates the Tat inhibitor’s efficacy as a potential therapeutic intervention for HIV-1 infection. Employing a one-dimensional impulsive differential equation model to determine the mathematically derived maximum concentration of the elongating complex (P2), the research considers the crucial aspect of optimal timing between successive dosages. A comparative analysis contrasts the effects of continuous dosing with impulse dosing of the Tat inhibitor, using numerical analysis to evaluate outcomes. The findings underscore the superior effectiveness of impulsive dosing over continuous dosing in inhibiting HIV-1 transcription. Visual representations of the model’s parameter sensitivities enhance understanding of the intricate physiological and biochemical processes within the system.
Practical implementation/social implications of the research
1. Treatment Optimization:
• Practical Implementation: Develop personalized treatment plans for individuals with HIV-1 based on the optimal control and impulsive approaches identified in the study.
• Social Implication: Improve the effectiveness of HIV-1 treatments, potentially leading to better health outcomes and a higher quality of life for individuals living with the virus.
2. Drug Administration Guidelines:
• Practical Implementation: Provide guidelines for healthcare professionals on the timing and dosage of Tat inhibitors using insights from the comparative study.
• Social Implication: Enhance the efficiency of drug administration, potentially reducing side effects and improving patient adherence to treatment regimens.
3. Public Health Planning:
• Practical Implementation: Incorporate the study’s findings into public health planning, considering the optimal and impulsive control strategies in broader HIV-1 prevention and treatment programs.
• Social Implication: Contribute to more effective and resource-efficient public health interventions, potentially reducing the overall burden of HIV-1 in communities.
4. Drug Development Strategies:
• Practical Implementation: Inform pharmaceutical companies and researchers about the comparative study results to guide the development of new HIV-1 inhibitors or improvements to existing drugs.
• Social Implication: Accelerate the development of more potent and targeted therapies, offering new options for managing HIV-1 infections.
5. Patient Education:
• Practical Implementation: Develop educational materials for individuals with HIV-1, explaining the importance of adherence to optimized treatment plans based on the study’s findings.
• Social Implication: Empower patients to actively participate in their treatment, potentially leading to better treatment outcomes and reduced transmission rates.
6. Policy Recommendations:
• Practical Implementation: Present policy recommendations to healthcare institutions and government agencies based on the study’s outcomes.
• Social Implication: Influence health policies to integrate the most effective strategies for HIV-1 transcription inhibition, potentially contributing to more efficient resource allocation and improved public health outcomes.
7. Global Health Impact:
• Practical Implementation: Collaborate with international health organizations to disseminate the study’s findings globally.
• Social Implication: Contribute to global efforts in controlling the HIV-1 pandemic, fostering collaboration and knowledge-sharing among nations.
8. Reduced Healthcare Costs:
• Practical Implementation: If the impulsive approach proves more cost-effective, healthcare systems can implement this strategy to potentially reduce the overall cost of HIV-1 treatment
• Social Implication: Alleviate financial burdens on both individuals and healthcare systems, making HIV-1 treatment more accessible
In summary, the practical implementation and social implications of this study extend from optimizing individual treatment plans to influencing global health policies, ultimately contributing to more effective HIV-1 management and improved public health outcomes.
Collaborations
- Prof. D C Dalal, Professor, Department of Mathematics, IIT Guwahati
- Prof. A K Sarkar, Professor, Centre for Mathematical Biology and Ecology, Department of Mathematics, Jadavpur University
- Dr L N Guin, Associate Professor, Department of Mathematics, Visva-Bharati
Future Prospects of the Research
- Mathematical Modelling of Cholesterol Dynamics.
- Mathematical Modelling of Muscle Regeneration.
- Mathematical Modelling of Bone Remodelling
- Mathematical Modelling of Glucose-Insulin Dynamics.
- Mathematical Modelling on HIV-1 Transcription.
- Mathematical Modelling of Population Dynamics for Patients suffering from Diabetes.

