The Department of Physics is glad to announce that Assistant Professor Dr Soumyajyoti Biswas and his PhD scholar Ms Diksha have published their article “Prediction of imminent failure using supervised learning in a fiber bundle model” in the Q1 journal, Physical Review E. Prediction of breakdown in disordered solids under external loading is a question of paramount importance to the stability of buildings and bridges to earthquakes. The researchers used numerical simulations of a model of disordered solids and recorded the time series of the avalanche sizes and energy bursts. They propose that a systematic analysis of these time series using supervised machine learning can predict the time of failure. Interestingly, the most important feature for such predictions turns out to be the measures of how unequal the avalanche sizes are.
Applying external stress on disordered materials beyond their mechanical limits results in their fracture. Hence it is important to know the limit or how the material behaves as it approaches the limit and the factors that influence it. The failure properties of materials are very distinct from other properties such as elasticity, in the sense that their predictions are not always straightforward. Predicting the failure in driven disordered systems is a long-standing problem in physics, engineering, and earth sciences. So, for understanding the fracture process and predicting the failure properties of the materials, a mathematical model (fibre bundle model) has been used.
They introduced the disorder to the system and generated the time series of avalanche size and energy bursts. Some inequality indices i.e., Hirsch index (h), Gini index (g) and recently introduced Kolkata index (k) were measured for the response statistics of the driven systems. These social inequalities are usually represented by the Lorenz function L(p), where p fraction of the population (events) possesses L(p) fraction of total wealth (avalanche mass) when the population (avalanche events) are arranged in the ascending order of their wealth (size). Based on these time series, the machine learning algorithm can predict the prior failure time of the system. So, they have used a supervised machine learning algorithm (with the above-mentioned indices as some of the features) to predict the failure time of the model. They observed that these inequality measures play an important role in making predictions.
Prediction of imminent fracture has its implications in a wide range of disciplines, including stability of mechanical structures (buildings, aircraft, bridges etc.), extraction of oil (fracking) to the largest scale of mechanical failure i.e., earthquakes. Here a supervised machine learning approach is used to make such predictions in numerical models. However, with the important features identified here for such predictions, such research can carry out similar predictions for experimental data. A follow-up of this work is being carried out by Ms Diksha with a group in Spain regarding the experimental verification. Their future research plans include applications of the methods developed here to be applied to real-life physical structures for their stability analysis and predictions of impending catastrophes.
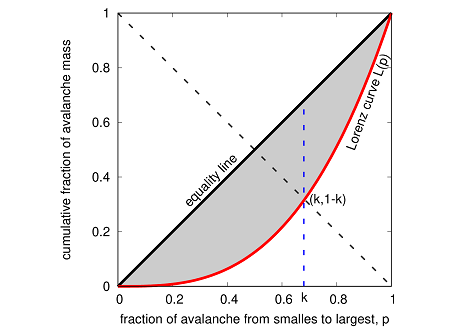
Illustration 1: A schematic diagram of the Lorenz function L(p)is shown, where L(p) denotes the cumulative fraction of the avalanche mass contained in the smallest p fraction of avalanches. If all avalanches were equal in size, this would be a diagonal straight line, called the equality line. The area between the equality line and the Lorenz curve (shaded area),therefore, is a measure of the inequality in the avalanche sizes. Two quantitative measures of such inequality are extracted from here, the ratio of the shaded area and that under the equality line (Gini index, g) and the crossing point of the opposite diagonal – from (0,1) to (1,0), shown in dashed line,and the Lorenz curve, giving the Kolkata index, k. 1 − k fraction of avalanches contain k fraction of the cumulative avalanche mass.

